Retrieve a fgpm from within a Xfgpm object

Retrieve the fgpm model with index (or rank) i from within a Xfgpm object. By evaluating this code in an environment containing suitable objects sIn, fIn and sOut we can re-create a fgpm object.

modelDef(
  object,
  ind,
  trace = TRUE,
  pbars = TRUE,
  control.optim = list(trace = TRUE)
)

Arguments

object

A Xfgpm object as created by fgpm_factory.

ind

The index (or rank) of the model in object.

trace

An optional boolean indicating whether funGp-native progress messages should be displayed. Default is TRUE. See the fgpm() documentation for more details.

pbars

An optional boolean indicating whether progress bars managed by fgpm() should be displayed. Default is TRUE. See the fgpm() documentation for more details.

control.optim

An optional list to be passed as the control argument to optim(), the function in charge of the non-linear optimization of the hyperparameters. Default is list(trace = TRUE). See the fgpm() documentation for more details.

Value

A parsed R code defining the fgpm model.

Details

The models are sorted by decreasing quality so i = 1 extracts the definition of the best model.

Note

Remind that the models are sorted by decreasing quality so i = 1 extracts the definition of the best model.

See also

The [[,Xfgpm-method that can also be used to re-create a fgpm object using the same data as that used to create the Xfgpm object in object.

Examples

## =========================================================================
## Using the pre-calculated object `xm` to save time. See `?xm` to re-create
## this object.
## =========================================================================

## 'xm@model' is the best 'fgpm' model in 'xm'
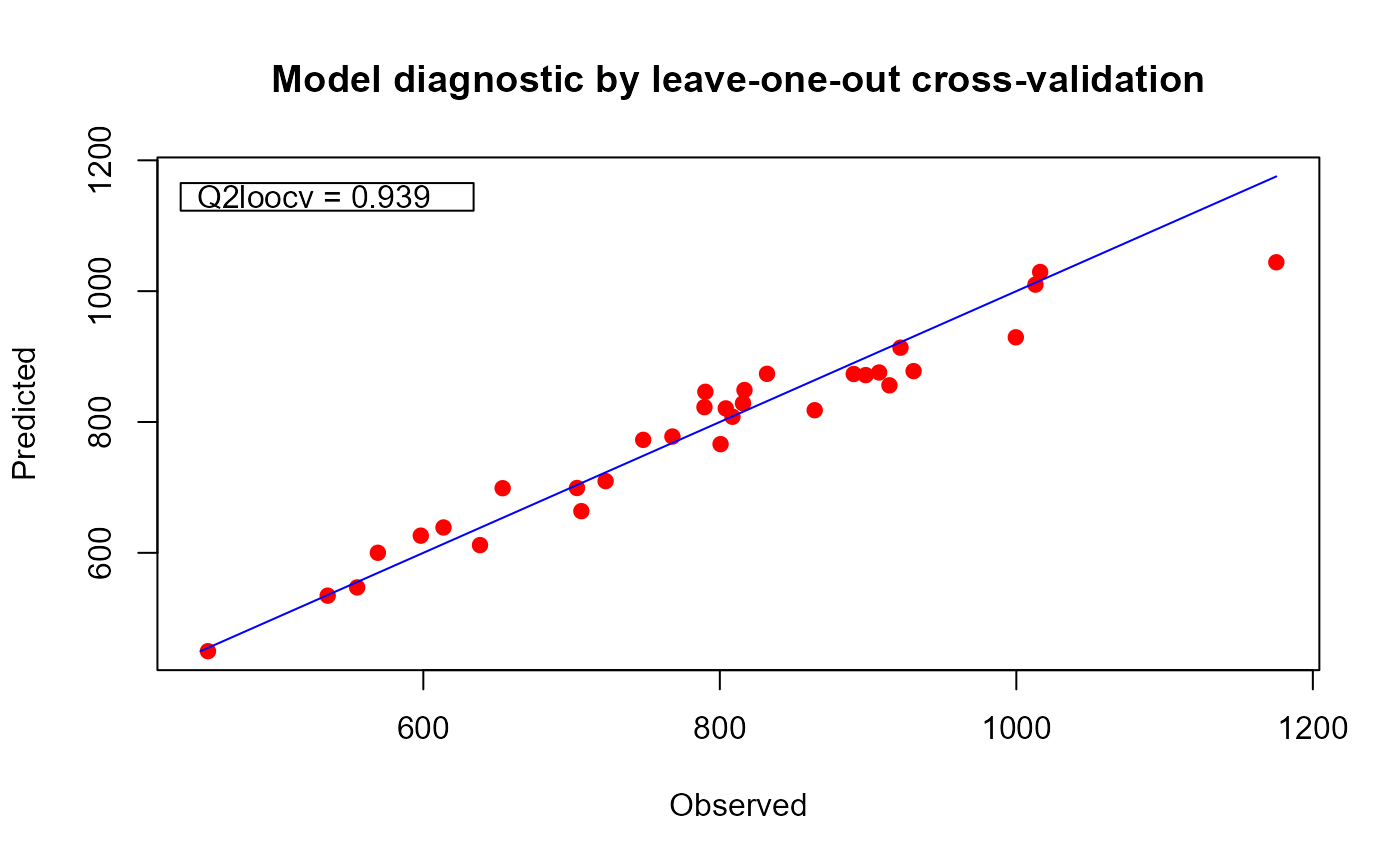
plot(xm@model)


## see the R code to use to recreate the model
modelDef(xm, i = 1)
#> expression(fgpm(sIn = sIn[, 2:5], fIn = fIn, sOut = sOut, f_disType = "L2_byindex", 
#>     f_pdims = c(1, 3), f_basType = "B-splines", kerType = "gauss", 
#>     trace = TRUE, pbars = TRUE, control.optim = list(trace = TRUE)))

if (FALSE) {
    ## Define new data in a list. Using an environment would also work,
    ## including the global environment, which is the default in  `eval`.
    L <- list()
    set.seed(341)
    n.new <- 3^5
    x1 <- x2 <- x3 <- x4 <- x5 <- seq(0, 1, length = n.new^(1/5))

    ## create the data objects required to fit the model
    L$sIn <- as.matrix(expand.grid(x1 = x1, x2 = x2, x3 = x3, x4 = x4, x5 = x5))
    L$fIn <- list(f1 = matrix(runif(n.new * 10), ncol = 10),
                   f2 = matrix(runif(n.new * 22), ncol = 22))
    L$sOut <- fgp_BB7(L$sIn, L$fIn, n.new)

    ## Now evaluate
    fgpm.new <- eval(modelDef(xm, i = 1), envir = L)
    plot(fgpm.new, main = "Re-created 'fgpm' model with different data")
    plot(xm[[1]], main = "Re-created 'fgpm' model with the same data")
}