This method enables simulation of Gaussian process values at any given set of points
based on a pre-built fgpm model. Check fgpm for information on how to create funGp models.
Arguments
- object
An object of class fgpm corresponding to the funGp model from which simulations must be performed.
- nsim
An optional integer indicating the number of samples to produce. Default is 1.
- seed
An optional value interpreted as an integer, that will be used as argument of
set.seedjust before simulating the response values.- sIn.sm
An optional matrix of scalar input coordinates at which the output values should be simulated. Each column is interpreted as a scalar input variable and each row as a coordinate. Either scalar input coordinates (sIn.sm), functional input coordinates (fIn.sm), or both must be provided.
- fIn.sm
An optional list of functional input coordinates at which the output values should be simulated. Each element of the list is interpreted as a functional input variable. Every functional input variable should be provided as a matrix with one curve per row. Either scalar input coordinates (sIn.sm), functional input coordinates (fIn.sm), or both must be provided.
- nugget.sm
An optional number corresponding to a numerical nugget effect. If provided, this number is added to the main diagonal of the simulation covariance matrix in order to prevent numerical instabilities during Cholesky decomposition. A small number in the order of 1e-8 is often enough. Default is 0.
- detail
An optional character specifying the extent of information that should be delivered by the method, to be chosen between
"light"(default) and"full". Light simulations produce a matrix of simulated output values, with as many rows as requested random samples. Full simulations produce a list with the matrix of simulated output values, along with the predicted mean, standard deviation and limits of the 95% confidence intervals at the simulation points.- ...
Not used.
Value
An object containing the data structures linked to simulations. For light simulations, the output will be a matrix of simulated output values, with as many rows as requested random samples. For full simulations, the output will be a list with the matrix of simulated output values, along with the predicted mean, standard deviation and limits of the 95% confidence intervals at the simulation points.
See also
* plot.simulate.fgpm for the simulation plot of a fgpm model;
* predict,fgpm-method for predictions based on a fgpm model;
* plot.predict.fgpm for the prediction plot of a fgpm model.
Examples
# light simulations _______________________________________________________________________
# building the model
set.seed(100)
n.tr <- 25
sIn <- expand.grid(x1 = seq(0,1,length = sqrt(n.tr)), x2 = seq(0,1,length = sqrt(n.tr)))
fIn <- list(f1 = matrix(runif(n.tr*10), ncol = 10), f2 = matrix(runif(n.tr*22), ncol = 22))
sOut <- fgp_BB3(sIn, fIn, n.tr)
m1 <- fgpm(sIn = sIn, fIn = fIn, sOut = sOut)
#> ** Presampling...
#> ** Optimising hyperparameters...
#> final value 2.841058
#> converged
#> The function value is the negated log-likelihood
#> ** Hyperparameters done!
# generating input data for simulation
n.sm <- 100
sIn.sm <- as.matrix(expand.grid(x1 = seq(0,1,length = sqrt(n.sm)),
x2 = seq(0,1,length = sqrt(n.sm))))
fIn.sm <- list(f1 = matrix(runif(n.sm*10), ncol = 10), matrix(runif(n.sm*22), ncol = 22))
# making light simulations
m1.sims_l <- simulate(m1, nsim = 10, sIn.sm = sIn.sm, fIn.sm = fIn.sm)
# plotting light simulations
plot(m1.sims_l)
 # full simulations ________________________________________________________________________
# building the model
set.seed(100)
n.tr <- 25
sIn <- expand.grid(x1 = seq(0,1,length = sqrt(n.tr)), x2 = seq(0,1,length = sqrt(n.tr)))
fIn <- list(f1 = matrix(runif(n.tr*10), ncol = 10), f2 = matrix(runif(n.tr*22), ncol = 22))
sOut <- fgp_BB3(sIn, fIn, n.tr)
m1 <- fgpm(sIn = sIn, fIn = fIn, sOut = sOut)
#> ** Presampling...
#> ** Optimising hyperparameters...
#> final value 2.841058
#> converged
#> The function value is the negated log-likelihood
#> ** Hyperparameters done!
# making full simulations
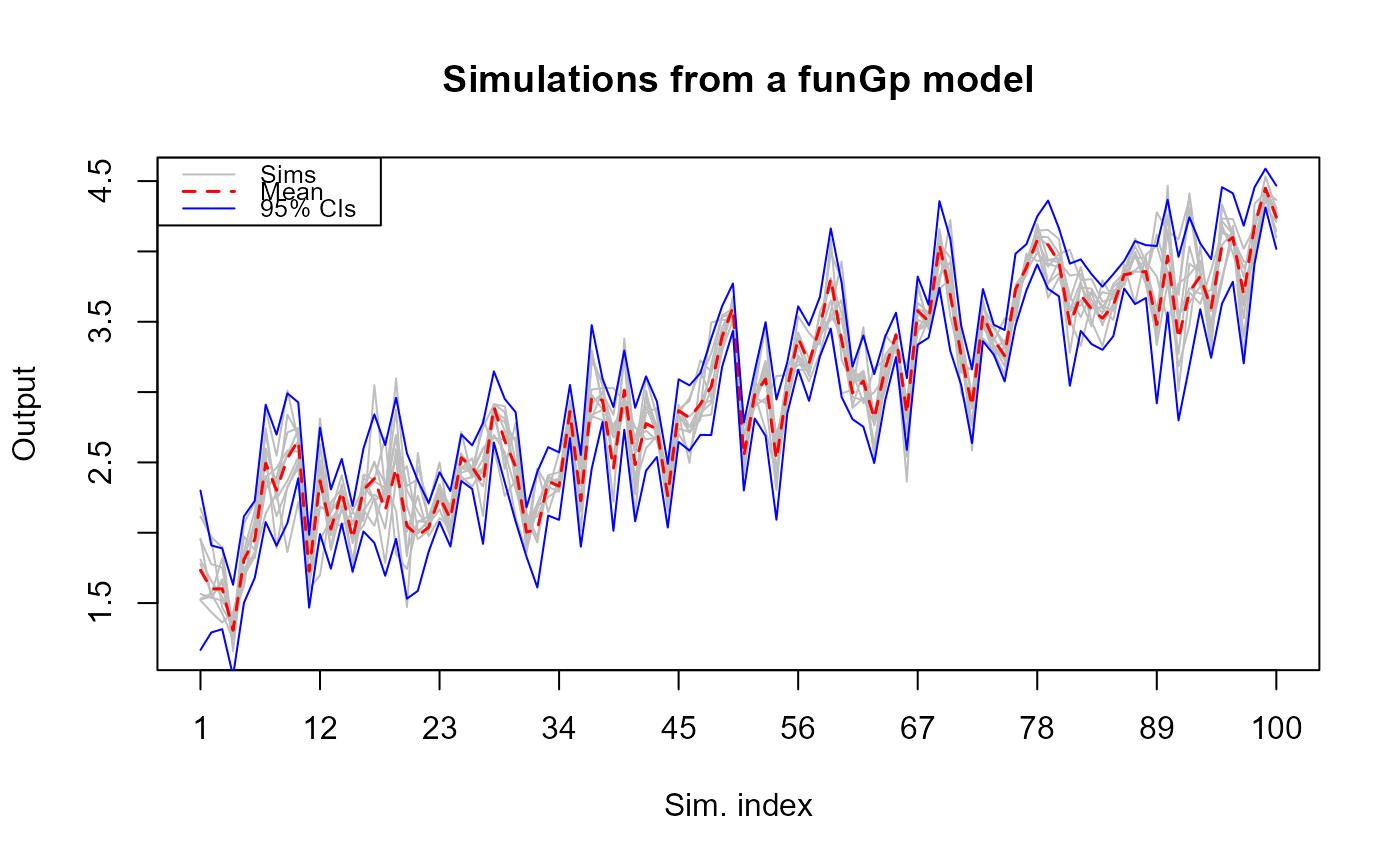
m1.sims_f <- simulate(m1, nsim = 10, sIn.sm = sIn.sm, fIn.sm = fIn.sm, detail = "full")
# checking content of the list
summary(m1.sims_f)
#> Length Class Mode
#> sims 1000 -none- numeric
#> mean 100 -none- numeric
#> sd 100 -none- numeric
#> lower95 100 -none- numeric
#> upper95 100 -none- numeric
# ~R output:~
# Length Class Mode
# sims 1000 -none- numeric
# mean 100 -none- numeric
# sd 100 -none- numeric
# lower95 100 -none- numeric
# upper95 100 -none- numeric
# plotting full simulations in full mode
plot(m1.sims_f)
# full simulations ________________________________________________________________________
# building the model
set.seed(100)
n.tr <- 25
sIn <- expand.grid(x1 = seq(0,1,length = sqrt(n.tr)), x2 = seq(0,1,length = sqrt(n.tr)))
fIn <- list(f1 = matrix(runif(n.tr*10), ncol = 10), f2 = matrix(runif(n.tr*22), ncol = 22))
sOut <- fgp_BB3(sIn, fIn, n.tr)
m1 <- fgpm(sIn = sIn, fIn = fIn, sOut = sOut)
#> ** Presampling...
#> ** Optimising hyperparameters...
#> final value 2.841058
#> converged
#> The function value is the negated log-likelihood
#> ** Hyperparameters done!
# making full simulations
m1.sims_f <- simulate(m1, nsim = 10, sIn.sm = sIn.sm, fIn.sm = fIn.sm, detail = "full")
# checking content of the list
summary(m1.sims_f)
#> Length Class Mode
#> sims 1000 -none- numeric
#> mean 100 -none- numeric
#> sd 100 -none- numeric
#> lower95 100 -none- numeric
#> upper95 100 -none- numeric
# ~R output:~
# Length Class Mode
# sims 1000 -none- numeric
# mean 100 -none- numeric
# sd 100 -none- numeric
# lower95 100 -none- numeric
# upper95 100 -none- numeric
# plotting full simulations in full mode
plot(m1.sims_f)
 # plotting full simulations in light mode
plot(m1.sims_f, detail = "light")
# plotting full simulations in light mode
plot(m1.sims_f, detail = "light")
